Induced topology
In topology and related areas of mathematics, an induced topology on a topological space is a topology which is "optimal" for some function from/to this topological space.
Contents |
Definition
Let 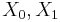 be sets,
be sets, 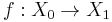 .
.
If 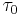 is a topology on
is a topology on 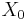 , then a topology induced on
, then a topology induced on 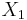 by
by  is
is 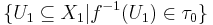 .
.
If 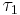 is a topology on
is a topology on 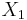 , then a topology induced on
, then a topology induced on 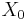 by
by  is
is 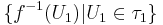 .
.
The easy way to remember the definitions above is to notice that finding an inverse image is used in both. This is because inverse image preserves union and intersection. Finding a direct image does not preserve intersection in general. Here is an example where this becomes a hurdle. Consider a set 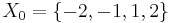 with a topology
with a topology 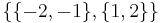 , a set
, a set 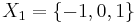 and a function
and a function 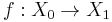 such that
such that 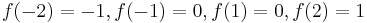 . A set of subsets
. A set of subsets 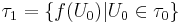 is not a topology, because
is not a topology, because 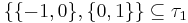 but
but 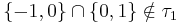 .
.
Properties
A topology 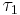 induced on
induced on 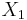 by
by  is the finest topology such that
is the finest topology such that  is continuous
is continuous 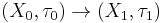 .
.
A topology 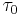 induced on
induced on 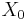 by
by  is the coarsest topology such that
is the coarsest topology such that  is continuous
is continuous 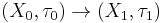 .
.
Examples
In particular, if  is an inclusion map, then
is an inclusion map, then 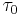 is a subspace topology.
is a subspace topology.
References
- Hu, Sze-Tsen (1969). Elements of general topology. Holden-Day.